Answer:
(a)
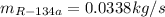
(b)
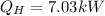
(c)
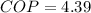
Step-by-step explanation:
Hello,
(a) In this part, we must know that the energy provided by the water equals the energy gained by the refrigerant-134a, thus:
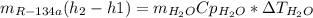
Now, water's heat capacity is about 4.18kJ/kg°C and the enthalpies at both the first and second state for the refrigerant-134a are computed as shown below, considering the first state as a vapor-liquid mixture (VLM) at 12°C and the second state as a saturated vapor (ST) at the same conditions:
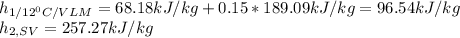
Next, solving the mass of water one obtains:
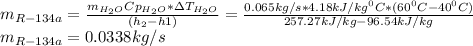
(b) Now, the energy balance allows us to compute the heat supply:
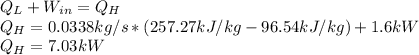
(c) Finally, the COP (coefficient of performance) is computed via:
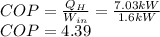
Best regards.