Question

Dy/dx if y = Ln (2x3 + 3x).

Answer 1

`(6x^2+3)/(2x^3+3x)`

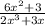
Explanation:

You need to apply the chain rule here.

There are few other requirements:

You will need to know how to differentiate
`\ln(u)`.

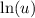You will need to know how to differentiate polynomials as well.

So here are some rules we will be applying:

Assume
`u=u(x) \text{ and } v=v(x)`

`(d)/(dx)\ln(u)=(1)/(u) \cdot (du)/(dx)`

`\text{ power rule } (d)/(dx)x^n=nx^(n-1)`

`\text{ constant multiply rule } (d)/(dx)c\cdot u=c \cdot (du)/(dx)`

`\text{ sum/difference rule } (d)/(dx)(u \pm v)=(du)/(dx) \pm (dv)/(dx)`

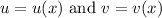
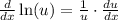
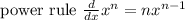
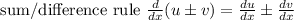
Those appear to be really all we need.

Let's do it:

`(d)/(dx)\ln(2x^3+3x)=(1)/(2x^3+3x) \cdot (d)/(dx)(2x^3+3x)`

`(d)/(dx)(\ln(2x^3+3x)=(1)/(2x^3+3x) \cdot ((d)/(dx)(2x^3)+(d)/(dx)(3x))`

`(d)/(dx)(\ln(2x^3+3x)=(1)/(2x^3+3x) \cdot (2 \cdot (dx^3)/(dx)+3 \cdot (dx)/(dx))`

`(d)/(dx)(\ln(2x^3+3x)=(1)/(2x^3+3x) \cdot (2 \cdot 3x^2+3(1))`

`(d)/(dx)(\ln(2x^3+3x)=(1)/(2x^3+3x) \cdot (6x^2+3)`

`(d)/(dx)(\ln(2x^3+3x)=(6x^2+3)/(2x^3+3x)`

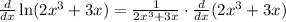
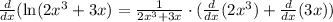
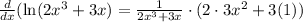
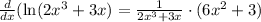
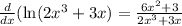
I tried to be very clear of how I used the rules I mentioned but all you have to do for derivative of natural log is derivative of inside over the inside.

Your answer is
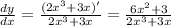`(dy)/(dx)=((2x^3+3x)')/(2x^3+3x)=(6x^2+3)/(2x^3+3x)`.