Answer:
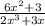
Explanation:
You need to apply the chain rule here.
There are few other requirements:
You will need to know how to differentiate
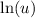 .
.
You will need to know how to differentiate polynomials as well.
So here are some rules we will be applying:
Assume
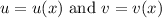
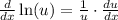
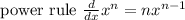
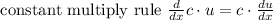
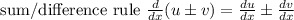
Those appear to be really all we need.
Let's do it:
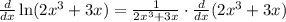
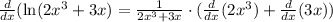
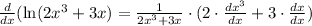
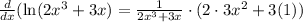
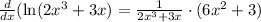
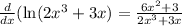
I tried to be very clear of how I used the rules I mentioned but all you have to do for derivative of natural log is derivative of inside over the inside.
Your answer is
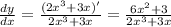 .
.