To find the x intercepts, we need to put the standard form equation into factored form.
Which two numbers multiply to -8 and add to -2?

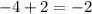
So the factored form is

That means the x intercepts are at

So now we have the x intercepts.
To find the vertex, we need to convert the standard form equation into vertex form.
The formula of vertex form is

Since the a value in the standard form equation is 1, the a value in vertex form is also one.
The h value can be found using the formula
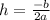
Which comes out to
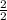 or 1.
or 1.
To find the k value, we can just plug in what we got for h back into the equation.
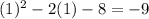
So the vertex is
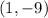 .
.
This also means the axis of symmetry is

Finally, to find the y intercept, we plug in 0 for x and solve.
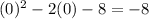
So the y intercept is
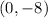 .
.