Question

Determine whether f(x) = –5x^2 – 10x + 6 has a maximum or a minimum value.

Find that value and explain how you know

Answer 1

First,

We are dealing with parabola since the equation has a form of,

`y=ax^2+bx+c`

Here the vertex of an up - down facing parabola has a form of,

`x_v=-(b)/(2a)`

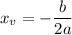
The parameters we have are,

`a=-5,b=-10, c=6`

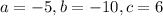
Plug them in vertex formula,

`x_v=-(-10)/(2(-5))=-1`

Plug in the
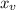`x_v` into the equation,

`y_v=-5(-1)^2-10(-1)+6=11`

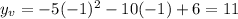
We now got a point parabola vertex with coordinates,

`(x_v, y_v)\Longrightarrow(-1,11)`

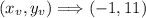
From here we emerge two rules:

• If
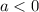  `a<0` then vertex is max value
• If
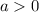  `a>0` then vertex is min value

So our vertex is minimum value since,

`a=-5\Longleftrightarrow a<0`

Hope this helps.

r3t40