First,
We are dealing with parabola since the equation has a form of,
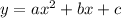
Here the vertex of an up - down facing parabola has a form of,
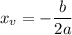
The parameters we have are,
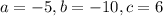
Plug them in vertex formula,
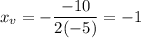
Plug in the
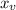 into the equation,
into the equation,
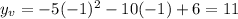
We now got a point parabola vertex with coordinates,
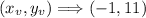
From here we emerge two rules:
- If
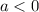 then vertex is max value
then vertex is max value - If
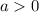 then vertex is min value
then vertex is min value
So our vertex is minimum value since,

Hope this helps.
r3t40