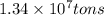Question

Be sure to answer all parts. The annual production of sulfur dioxide from burning coal and fossil fuels, auto exhaust, and other sources is about 26 million tons. The equation for the reaction is S(s) + O2(g) → SO2(g) If 2.68 × 107 tons of sulfur dioxide formed, how many tons of sulfur were present in the original materials? Assume 100% yield. × 10 tons Enter your answer in scientific notation.

Answer 1

Answer: The amount of sulfur present in the original material is
`1.34* 10^7tons`

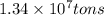
Step-by-step explanation:

Converting given amount of mass in tons to grams, we use the conversion factor:

1 ton = 907185 g .......(1)

So,
`2.68* 10^7=2.431* 10^(13)g`

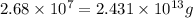
To calculate the number of moles, we use the equation:

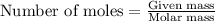`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}` ......(2)

Given mass of sulfur dioxide =
`2.431* 10^(13)g`

Molar mass of sulfur dioxide = 64 g/mol

Putting values in above equation, we get:

`\text{Moles of sulfur dioxide}=(2.431* 10^(13)g)/(64g/mol)=3.79* 10^9mol`

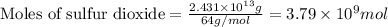
For the given chemical reaction:

`S(s)+O_2(g)\rightarrow SO_2(g)`

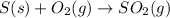
By Stoichiometry of the reaction:

1 mole of sulfur dioxide is produced from 1 mole of sulfur

So,
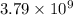`3.79* 10^9` moles of sulfur dioxide will be produced from =
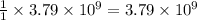`(1)/(1)* 3.79* 10^9=3.79* 10^9` moles of sulfur.

Now, calculating the mass of sulfur using equation 2:

Moles of sulfur =
`3.79* 10^9mol`

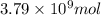
Molar mass of sulfur = 32 g/mol

Putting values in equation 2, we get:

`3.79* 10^9mol=\frac{\text{Mass of sulfur}}{32g/mol}\\\\\text{Moles of sulfur}=121.54* 10^(11)g`

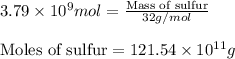
Converting this value in tons using conversion factor 1, we get:

`\Rightarrow ((1ton)/(907185g))* 121.54* 10^(11)g\\\\\Rightarrow 13397491.6tons=1.34* 10^7tons`

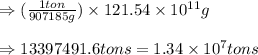
Hence, the amount of sulfur present in the original material is
`1.34* 10^7tons`