Answer: The amount of sulfur present in the original material is

Step-by-step explanation:
Converting given amount of mass in tons to grams, we use the conversion factor:
1 ton = 907185 g .......(1)
So,
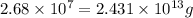
To calculate the number of moles, we use the equation:
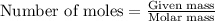 ......(2)
......(2)
Given mass of sulfur dioxide =

Molar mass of sulfur dioxide = 64 g/mol
Putting values in above equation, we get:
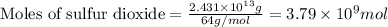
For the given chemical reaction:
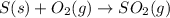
By Stoichiometry of the reaction:
1 mole of sulfur dioxide is produced from 1 mole of sulfur
So,
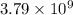 moles of sulfur dioxide will be produced from =
moles of sulfur dioxide will be produced from =
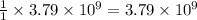 moles of sulfur.
moles of sulfur.
Now, calculating the mass of sulfur using equation 2:
Moles of sulfur =
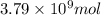
Molar mass of sulfur = 32 g/mol
Putting values in equation 2, we get:
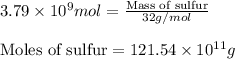
Converting this value in tons using conversion factor 1, we get:
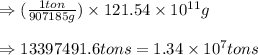
Hence, the amount of sulfur present in the original material is
