Question

Write the slope-intercept form of the equation that passes through the point (0,-3) and is perpendicular to the line y = 2x - 6

Answer 1

`y=-(1)/(2)x -3`

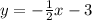
Explanation:

The slope-intercept form of the equation of a line has the following form:

`y=mx + b`

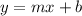
Where m is the slope of the line and b is the intercept with the y axis

In this case we look for the equation of a line that is perpendicular to the line

`y = 2x - 6`.

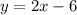By definition If we have the equation of a line of slope m then the slope of a perpendicular line will have a slope of
`-(1)/(m)`

In this case the slope of the line
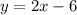`y = 2x - 6` is
`m=2`:

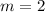Then the slope of the line sought is:
`m=-(1)/(2)`

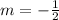
The intercept with the y axis is:

If we know a point
`(x_1, y_1)` belonging to the searched line, then the constant b is:

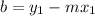`b=y_1-mx_1` in this case the poin is: (0,-3)

Then:

`b= -3 -((1)/(2))(0)\\\\b=-3`

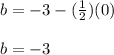
finally the equation of the line is:

`y=-(1)/(2)x-3`

Answer 2

For this case we have that by definition, the equation of a line of the slope-intersection form is given by:

`y = mx + b`

Where:

m: It's the slope

b: It is the cutoff point with the y axis

By definition, if two lines are perpendicular then the product of their slopes is -1.

We have the following line:

`y = 2x-6`

Then
`m_ {1} = 2`

The slope of a perpendicular line will be:

`m_ {1} * m_ {2} = - 1\\m_ {2} = \frac {-1} {m_ {1}}\\m_ {2} = - \frac {1} {2}`

Thus, the equation of the line will be:

`y = - \frac {1} {2} x + b`

We substitute the given point and find "b":

`-3 = - \frac {1} {2} (0) + b\\-3 = b`

Finally the equation is:

`y = - \frac {1} {2} x-3`

Answer:

`y = - \frac {1} {2} x-3`