Question

Relative to the ground, a car has a velocity of 15.3 m/s, directed due north. Relative to this car, a truck has a velocity of 22.5 m/s, directed 52.0° north of east. What is the magnitude of the truck's velocity relative to the ground

Answer 1

The magnitude of the truck's velocity relative to the ground is 35.82 m/s.

Step-by-step explanation:

Given that,

Velocity of car relative to ground = 15.3 m/s

Velocity of truck relative to car = 22.5 m/s

We need to calculate the magnitude of the truck's velocity relative to the ground

We need to calculate the x component of the velocity

`v_(x)=22.5\cos\theta`

`v_(x)=22.5\cos52^(\circ)`

`v_(x)=13.852\ m/s`

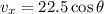
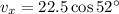
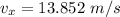
We need to calculate the y component of the velocity

`v_(y)=15.3+22.5\sin\theta`

`v_(y)=15.3+22.5\sin52^(\circ)`

`v_(y)=33.030\ m/s`

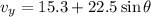
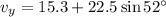
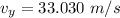
Using Pythagorean theorem

`|v|=\sqrt{v_(x)^2+v_(y)^2}`

`|v|=√((13.852)^2+(33.030)^2)`

`|v|=35.82\ m/s`

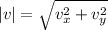
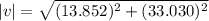
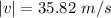
Hence, The magnitude of the truck's velocity relative to the ground is 35.82 m/s.