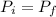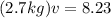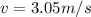Answer:
Part a)
P = 8.23 kg m/s
Part b)
v = 3.05 m/s
Step-by-step explanation:
Part a)
momentum of cart 1 is given as
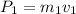
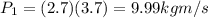
Momentum of cart 2 is given as
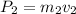
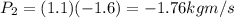
Now total momentum of both carts is given as


Part b)
Since two carts are moving towards each other due to mutual attraction force and there is no external force on two carts so here momentum is always conserved
so here we will have