Answer:
A. In the graph,
Go 5 units left side from the origin in the x-axis then from that point go downward 6 unit, we will get (-5, -6),
Now, go 10 unit right from the origin in the x-axis then from that point go upward 3 unit, we will get (10, 3),
B. The slope of the line passes through (-5, -6) and (10, 3),
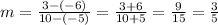
C. Since, the equation of a line passes through
 with slope m is,
with slope m is,

Thus, the equation of the line is,
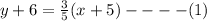
For y-intercept,
x = 0,

That is, y-intercept is -3.
D. From equation (1),
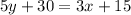
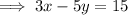
Which is the required linear function.