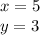Answer: option c
Explanation:
Find the x-intercept and y-intercept of each line.
To find the x-intercept, substitute
 into the equation and solve for "x".
into the equation and solve for "x".
To find the y-intercept, substitute
 into the equation and solve for "y".
into the equation and solve for "y".
- For the first equation:
x-intercept
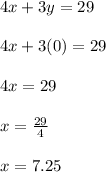
y-intercept
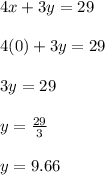
Graph a line that passes through the points (7.25, 0) and (0, 9.66)
- For the second equation:
x-intercept
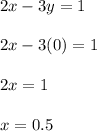
y-intercept
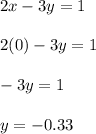
Graph a line that passes through the points (0.5, 0) and (0, -0.33)
Observe the graph attached. You can see that point of intersection of the lines is (5,3); then this is the solution of the system. Therefore: