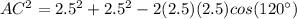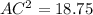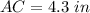Question

AB id a diameter of a circle centered at o. C is a point on the circle such that angle BOC is 60 degrees.If the diameter of the circle is 5 inches the length of the chord ac expressed in inches is

Answer 1

`AC=4.3\ in`

Explanation:

see the attached figure to better understand the problem

we know that

The triangle AOC is an isosceles triangle

OA=OC=5/2=2.5 in -----> the radius of the circle

∠AOC=180°-60°=120°

∠CAO=∠ACO=120°/2=60°

Applying the law of cosines find the length of the chord AC

`AC^(2)=OA^(2)+OC^(2)-2(OA)(OC)cos(120\°)`

substitute

`AC^(2)=2.5^(2)+2.5^(2)-2(2.5)(2.5)cos(120\°)`

`AC^(2)=18.75`

`AC=4.3\ in`