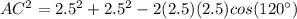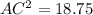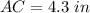Answer:
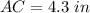
Explanation:
see the attached figure to better understand the problem
we know that
The triangle AOC is an isosceles triangle
OA=OC=5/2=2.5 in -----> the radius of the circle
∠AOC=180°-60°=120°
∠CAO=∠ACO=120°/2=60°
Applying the law of cosines find the length of the chord AC
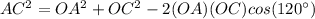
substitute