Answer:
The required standard form of ellipse is
 .
.
Explanation:
The standard form of an ellipse is

Where, (h,k) is center of the ellipse.
It is given that the center of the circle is (0,0), so the standard form of the ellipse is
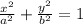 .... (1)
.... (1)
If a>b, then coordinates of vertices are (±a,0), coordinates of co-vertices are (0,±b) and focus (±c,0).
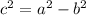 .... (2)
.... (2)
If a<b, then coordinates of vertices are (0,±b), coordinates of co-vertices are (±a,0) and focus (0,±c).
 .... (3)
.... (3)
It is given that co-vertex of the ellipse at (5, 0); focus at (0, 3). So, a<b we get
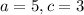
Substitute a=5 and c=3 these values in equation (3).
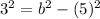
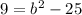
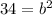
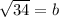
Substitute a=5 and
 in equation (1), to find the required equation.
in equation (1), to find the required equation.
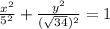

Therefore the required standard form of ellipse is
 .
.