Question

The midpoint of a segment is (−2,−3) and one endpoint is (3,0) . Find the coordinates of the other endpoint.

A. (8, 3)
B. (-7, 3)
C. (8, -6)
D. (-7, -6)

Answer 1

To work out the mid point of two points you, add the x coordinates and divide by 2, and you take the y coordinates and divide by two:

So:

`midpoint = (sum.of.x-coords)/(2),  (sum.of.y-coords)/(2)`

------------------------------------

So the x-coords of the midpoint is:

`(sum.of.x-coords)/(2)`

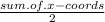
and

y -coords of midpoint is:

`(sum.of.y-coords)/(2)`

------------------------------------

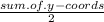
However, in this question we are trying to work out one of the endpoints.

First let's say that the coordinates of the missing endpoint is:

(x , y)

_____________________________________________

That means that the x-coords of the midpoint of (x, y) and the other endpoint (3, 0) is :

`(3 + x)/(2)`

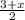
However, we already know the x-coord of the midpoint ( it's -2). So we can form an equation to workout x:

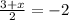`(3 + x)/(2) = -2` (multiply both sides by 2)

`3 + x = -4` (subtract 3 from both sides)

`x = -7`

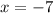
This is the x-coord of the other endpoint

_______________________________________________

Let's do the same for the y coordinates:

We know y coords for the midpoint of (x, y) and (3, 0) is:

`(0 + y)/(2)`

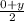
But we also know the ycoord is -3. So we can form an equation and solve for y:

`(0+y)/(2) = -3`

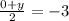
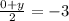`(0 + y)/(2) = -3` (multiply both sides by 2)

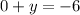`0 + y = -6` (simplify)

`y = -6`

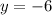
This is the y-coord of the other endpoint

___________________________________

Now we just put these coords together to get the coordinate of the other endpoint:

Endpoint is at:

(x, y) (substitute in values that we worked out)

= (-7, -6)

_________________________________________________

Answer:

D. (-7, -6)

________________________________________________

Note:

If there is anything you don't quite understand or was unclear

- please don't hesitate to ask below in the comments.

Answer 2

The midpoint can be defined using formula,

`M(x_m=(x_1+x_2)/(2),y_m=(y_1+y_2)/(2))`

So by knowing
`x_m, x_1` and
`y_m, y_1` we can calculate
`x_2, y_2`

First we must derive two equations,

`x_m=(x_1+x_2)/(2)\Longrightarrow x_2=2x_m-x_1`

and

`y_m=(y_1+y_2)/(2)\Longrightarrow y_2=2y_m-y_1`

Then just put in the data,

`x_2=2\cdot(-2)-3=-7`

`y_2=2\cdot(-3)-0=-6`

So the other endpoint has coordinates
`(x,y)\Longrightarrow(-7, -6)` therefore the answer is D.

Hope this helps.

r3t40