To work out the mid point of two points you, add the x coordinates and divide by 2, and you take the y coordinates and divide by two:
So:
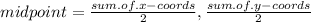
------------------------------------
So the x-coords of the midpoint is:
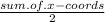
and
y -coords of midpoint is:
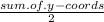
------------------------------------
However, in this question we are trying to work out one of the endpoints.
First let's say that the coordinates of the missing endpoint is:
(x , y)
_____________________________________________
That means that the x-coords of the midpoint of (x, y) and the other endpoint (3, 0) is :
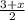
However, we already know the x-coord of the midpoint ( it's -2). So we can form an equation to workout x:
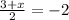 (multiply both sides by 2)
(multiply both sides by 2)
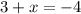 (subtract 3 from both sides)
(subtract 3 from both sides)
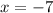
This is the x-coord of the other endpoint
_______________________________________________
Let's do the same for the y coordinates:
We know y coords for the midpoint of (x, y) and (3, 0) is:
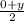
But we also know the ycoord is -3. So we can form an equation and solve for y:
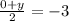
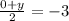 (multiply both sides by 2)
(multiply both sides by 2)
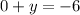 (simplify)
(simplify)
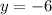
This is the y-coord of the other endpoint
___________________________________
Now we just put these coords together to get the coordinate of the other endpoint:
Endpoint is at:
(x, y) (substitute in values that we worked out)
= (-7, -6)
_________________________________________________
Answer:
D. (-7, -6)
________________________________________________
Note:
If there is anything you don't quite understand or was unclear
- please don't hesitate to ask below in the comments.