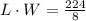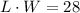Question

the length of a rectangle is 5 centimeters less than twice its width. It’s area is 28 square centimeters. Find the dimensions of the rectangle

Answer 1

It didn't saying anything about rounding but the the dimensions in there exact form are:

`L=(-5+√(249))/(2) \text{ cm}`

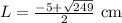
and

`W=(5 + √(249))/(4) \text{ cm }`.

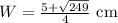Now if they said to round to the nearest hundredths the dimensions in this rounded form would be:

L=5.39 cm and W=5.19 cm

(Check your question again and see if you meant what you have)

Explanation:

L is 5 less than twice W

L = 2W-5

Area of rectangle=L*W

Area is 28 means L*W=28.

I'm going to insert L=2W-5 into L*W=28 giving me

(2W-5)*W=28

Distribute

2W^2-5W=28

Subtract 28 on both sides

2W^2-5W-28=0

a=2

b=-5

c=-28

We are going to use the quadratic formula.

Plug in...

`W=(-b \pm √(b^2-4ac))/(2a)\\\\W=(5 \pm √((-5)^2-4(2)(-28)))/(2(2))\\\\W=(5 \pm √(25+224))/(4)\\\\W=(5 \pm √(249))/(4)`

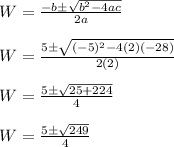
W needs to be positive so
`W=(5 + √(249))/(4)`

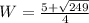
And
`L=2W-5=2((5 + √(249))/(4))-5`

`L=(5+√(249))/(2)-5`

`L=(5+√(249))/(2)-(10)/(2)`

`L=(-5+√(249))/(2)`

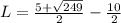
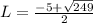
Does L*W=28?

Let's check.

`L \cdot W=(-5+√(249))/(2) \cdot (5 + √(249))/(4)`

`L \cdot W=(249-25)/(8)`

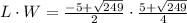
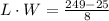
In the last step, I was able to do a quick multiplication because I was multiplying conjugates. (a+b)(a-b)=a^2-b^2.

`L \cdot W=( 224)/(8)`

`L \cdot W=28`