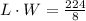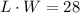Answer:
It didn't saying anything about rounding but the the dimensions in there exact form are:
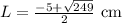
and
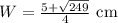 .
.
Now if they said to round to the nearest hundredths the dimensions in this rounded form would be:
L=5.39 cm and W=5.19 cm
(Check your question again and see if you meant what you have)
Explanation:
L is 5 less than twice W
L = 2W-5
Area of rectangle=L*W
Area is 28 means L*W=28.
I'm going to insert L=2W-5 into L*W=28 giving me
(2W-5)*W=28
Distribute
2W^2-5W=28
Subtract 28 on both sides
2W^2-5W-28=0
a=2
b=-5
c=-28
We are going to use the quadratic formula.
Plug in...
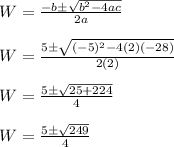
W needs to be positive so
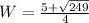
And
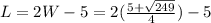
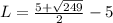
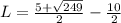
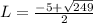
Does L*W=28?
Let's check.
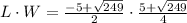
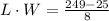
In the last step, I was able to do a quick multiplication because I was multiplying conjugates. (a+b)(a-b)=a^2-b^2.