Question

The waiting times between a subway departure schedule and the arrival of a passenger are uniformly distributed between 0 and 6 minutes. Find the probability that a randomly selected passenger has a waiting time greater than 2.25 minutes. Find the probability that a randomly selected passenger has a waiting time greater than 2.25 minutes.

Answer 1

Explanation:

the answer is 0.625 reason is the probability is 62.5% and when you take

(6-2.25)/(6-0)

= (3.75)/(6)

=0.625

Answer 2

Answer: 0.375

Explanation:

The given interval : (0,6) [in minutes]

Let X represents the waiting time of a passenger.

We know that the cumulative uniform distribution function for interval (a,b) is given by :_

`F(x)=\begin{cases}0,&\text{ for } x<a\\(x-a)/(b-a),& \text{for } a\leq x\leq 1\\1,& \text{for }x>b\end{cases}`

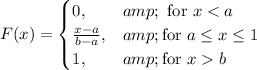
Then , the probability that a randomly selected passenger has a waiting time greater than 2.25 minutes. is given by :_

`P(2.25<x)=(2.25-0)/(6-0)=0.375`

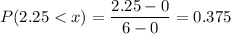
Hence, the required probability : 0.375