Answer:

Explanation:
1st boat:
Parabola equation:

The x-coordinate of the vertex:
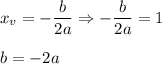
Equation:

The y-coordinate of the vertex:

Parabola passes through the point (-8,1), so
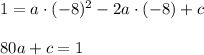
Solve:
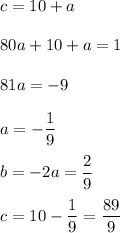
Parabola equation:
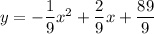
2nd boat:
Parabola equation:

The x-coordinate of the vertex:
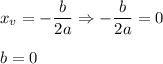
Equation:

The y-coordinate of the vertex:
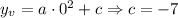
Parabola passes through the point (-8,1), so
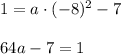
Solve:
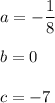
Parabola equation:

System of two equations:
