Answer:
True.
Explanation:
Let's use the picture I made.
I used degrees instead...
tan(90-x)= b/a . I did opposite over adjacent for the angle labeled 90-x which is that angle's measurement.
cot(x)=b/a . I did adjacent over opposite for the angle labeled 90 which is that angle's measurement.
Now this is also known as a co-function identity.
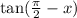
Rewrite using quotient identity for tangent

Rewrite using difference identities for sine and cosine
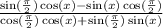
sin(pi/2)=1 while cos(pi/2)=0
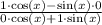
Do a little basic algebra
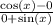
More simplification
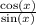
This is quotient identity for cotangent
