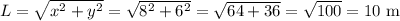Question

The top of a ladder slides down a vertical wall at a rate of 0.675 m/s. At the moment when the bottom of the ladder is 6 m from the wall, it slides away from the wall at a rate of 0.9 m/s. How long is the ladder?

Answer 1

The length of ladder=8m.

Explanation:

Given

The rate at which the top of a ladder slides down a vertical wall,
`\frac{\mathrm{d}z}{\mathrm{d}t}`= 0.675m/s

The distance of bottom of ladder from the wall,x=6m

The rate at which it slides away from the wall ,
`\frac{\mathrm{d}x}{\mathrm{d}t}`=0.9m/s

Let length of ladder =z

Length of wall=y

Distance between foot of ladder and wall=x

By using pythogorous theorem

`x^2+y^2=z^2`

Differentiate w.r.t time

`x\frac{\mathrm{d}x}{\mathrm{d}t}=z\frac{\mathrm{d}z}{\mathrm{d}t}`

y does not change hence,
`\frac{\mathrm{d}y}{\mathrm{d}t}=0`

`6* 0.9=z* 0.675`

`z=(5.4)/(0.675)`

z=8 m

Hence, the length of ladder=8m.

Answer 2

The length of the ladder is 10 m.

Explanation:

Let x shows the distance of the top of ladder from the bottom of base of the wall, y shows the distance of the bottom of ladder from the base of the wall and l is the length of the ladder,

Given,

`(dx)/(dt)=-0.675\text{ m/s}`

`(dy)/(dt)=0.9\text{ m/s}`

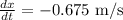
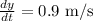
y = 6 m,

Since, the wall is assumed perpendicular to the ground,

By the pythagoras theorem,

`l^2=x^2+y^2`

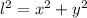
Differentiating with respect to t ( time ),

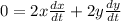`0=2x(dx)/(dt)+2y(dy)/(dt)` ( the length of wall would be constant )

By substituting the value,

`0=2x(-0.675)+2(6)(0.9)`

`0=-1.35x+10.8`

`\implies x=(10.8)/(1.35)=8`

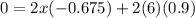
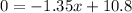
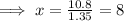
Hence, the length of the ladder is,

`L=√(x^2+y^2)=√(8^2+6^2)=√(64+36)=√(100)=10\text{ m}`