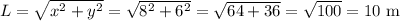Answer:
The length of the ladder is 10 m.
Explanation:
Let x shows the distance of the top of ladder from the bottom of base of the wall, y shows the distance of the bottom of ladder from the base of the wall and l is the length of the ladder,
Given,
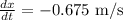
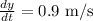
y = 6 m,
Since, the wall is assumed perpendicular to the ground,
By the pythagoras theorem,
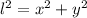
Differentiating with respect to t ( time ),
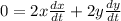 ( the length of wall would be constant )
( the length of wall would be constant )
By substituting the value,
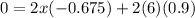
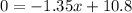
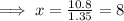
Hence, the length of the ladder is,