Question

Which values of a and b make the following equation true? (5x7y2)(-4x4y5)=-20xayb

Answer 1

a=11, b=7

i just took the test on edge2020

Answer 2

The values of a and b are a = 11 , b = 7

Explanation:

* Lets explain how to solve the problem

* In the exponential functions we have some rules

1- In multiplication if they have same base we add the power

# Ex: b^m × b^n = b^(m + n) ⇒ b is the base , m and n are the powers

2- In division if they have same base we subtract the power

# Ex: b^m ÷ b^n = b^(m – n) ⇒ b is the base , m and n are the powers

3- If we have power over power we multiply them

# Ex: (b^m)^n = b^(mn) ⇒ b is the base , m and n are the powers

* Lets solve the problem

∵ The equation is
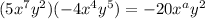`(5x^(7)y^(2))(-4x^(4)y^(5))=-20x^(a)y^(2)` ⇒ (1)

- At first multiply the coefficients

∵ -4 × 5 = -20

- Multiply the base x

∵
`(x^(7))(x^(4))=x^(7+4)=x^(11)`

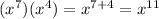
- Multiply the base y

∵
`(y^(2))(y^(5))=y^(2+5)=y^(7)`

∴
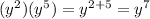
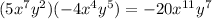`(5x^(7)y^(2))(-4x^(4)y^(5))=-20x^(11)y^(7)` ⇒ (2)

- By comparing (1) and (2)

∴ a = 11 and b = 7

* The values of a and b are a = 11 , b = 7