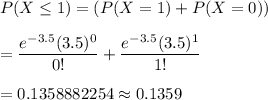Answer: (a) 0.8641
(b) 0.1359
Explanation:
Given : The monthly worldwide average number of airplane crashes of commercial airlines
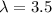
We use the Poisson distribution for the given situation.
The Poisson distribution formula for probability is given by :-
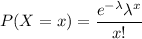
a) The probability that there will be at least 2 such accidents in the next month is given by :-
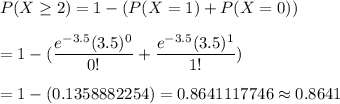
b) The probability that there will be at most 1 accident in the next month is given by :-