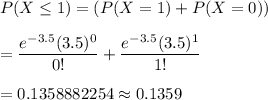8) The monthly worldwide average number of airplane crashes of commercial airlines is 3.5. What is the probability that there will be (a) at least 2 such accidents in the next m…

Question

asked Aug 6, 2020 195k views

1 Answer

Paul Beesley · Answer 1 · 2020-08-12T12:37:10+0000

Answer: (a) 0.8641

(b) 0.1359

Explanation:

Given : The monthly worldwide average number of airplane crashes of commercial airlines
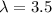
$\lambda= 3.5$

We use the Poisson distribution for the given situation.

The Poisson distribution formula for probability is given by :-

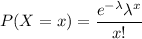
$P(X=x)=(e^(-\lambda)\lambda^x)/(x!)$

a) The probability that there will be at least 2 such accidents in the next month is given by :-

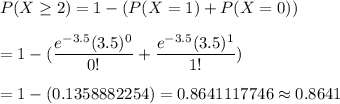
$P(X\geq2)=1-(P(X=1)+P(X=0))\\\\=1-((e^(-3.5)(3.5)^0)/(0!)+(e^(-3.5)(3.5)^1)/(1!))\\\\=1-(0.1358882254)=0.8641117746\approx0.8641$

b) The probability that there will be at most 1 accident in the next month is given by :-

$P(X\leq1)=(P(X=1)+P(X=0))\\\\=(e^(-3.5)(3.5)^0)/(0!)+(e^(-3.5)(3.5)^1)/(1!)\\\\=0.1358882254\approx0.1359$