Question

How many integers between 10000 and 99999, inclusive, are divisible by 3 or
5 or 7?

Answer 1

Answer: Hence, there are approximately 48884 integers are divisible by 3 or 5 or 7.

Explanation:

Since we have given that

Integers between 10000 and 99999 = 99999-10000+1=90000

n( divisible by 3) =
`(90000)/(3)=30000`

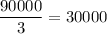
n( divisible by 5) =
`(90000)/(5)=18000`

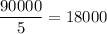
n( divisible by 7) =
`(90000)/(7)=12857.14`

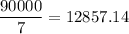
n( divisible by 3 and 5) = n(3∩5)=
`(90000)/(15)=6000`

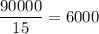
n( divisible by 5 and 7) = n(5∩7) =
`(90000)/(35)=2571.42`

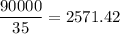
n( divisible by 3 and 7) = n(3∩7) =
`(90000)/(21)=4285.71`

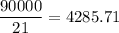
n( divisible by 3,5 and 7) = n(3∩5∩7) =
`(90000)/(105)=857.14`

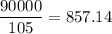
As we know the formula,

n(3∪5∪7)=n(3)+n(5)+n(7)-n(3∩5)-n(5∩7)-n(3∩7)+n(3∩5∩7)

`=30000+18000+12857.14-6000-2571.42-4258.71+857.14\\\\=48884.15`

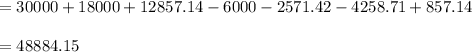
Hence, there are approximately 48884 integers are divisible by 3 or 5 or 7.