Question

Determine whether S is a basis for P3. S = {4t - 12,5 +t3,5 +3t,-3t2 +2/3

Answer 1

Yes , S is a basis for
`P_3`.

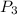Explanation:

Given

S=
`\left\{4t-12,5+t^3,5+3t,-3t^2+(2)/(3)\righ\}`.

We can make a matrix

Let A=
`\begin{bmatrix}-12&4&0&0\\5&0&0&1\\5&3&0&0\\(2)/(3)&0&-3&0\end{bmatrix}`

All rows and columns are linearly indepedent and S span
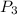`P_3`.Hence, S is a basis of
`P_3`

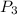
Linearly independent means any row or any column should not combination of any rows or columns.

Because a subset of V with n elements is a basis if and only if it is linearly independent.

Basis:- If B is a subset of a vector space V over a field F .B is basis of V if satisfied the following conditions:

1.The elements of B are linearly independent.

2.Every element of vector V spanned by the elements of B.