Question

Which expression is a sum of cubes?

Answer 1

`- 27 {a}^(3) {b}^(6) + 8 {a}^(9) {b}^(12)`

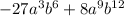
EXPLANATION

When we can write an expression in the form

`{(x)}^(3) + {(y)}^(3)`

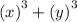
then it is a sum of cubes.

To write a given sum as sum of cubes, then the coefficients of the terms should cube be numbers and the exponents of any power should be a multiple of 3.

This tells us that the first option will be the best choice.

`- 27 {a}^(3) {b}^(6) + 8 {a}^(9) {b}^(12)`

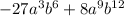
We can rewrite this as:

`{ (- 3)}^(3) {a}^(3) {b}^(2 * 3) + {2}^(3) {a}^(3 * 3) {b}^(4 * 3)`

We apply this property of exponents:

`({a}^(m) )^(n) = {a}^(mn)`

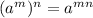
This gives us

`{( - 3a {b}^(2)) }^(3) + {(2{a}^(3) {b}^(4) })^(3)`

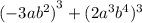
Therefore the correct option is A

Answer 2

-27a³b⁶+ 8a⁹b¹²

Explanation:

In the expression above -27 is a perfect cube of -3, 8 is a perfect cube of 2.

The exponents of a and b in both terms in the expression are divisible by 3.

The cube root of x, that is ∛xⁿ=x∧(n/3) where n is an integer.