Answer:
The function which is an exponential decay function is:
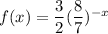
Explanation:
We know that an exponential function is in the form of:

where a>0 and if 0<b<1 then the function is a exponential decay function.
and if b>1 then the function is a exponential growth function.
a)
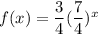
Here
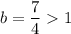
Hence, the function is a exponential growth function.
b)
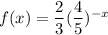
We know that:
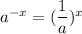
Hence, we have the function f(x) as:
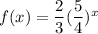
Here
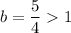
Hence, the function is a exponential growth function.
c)
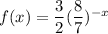
We know that:
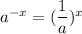
Hence, we have the function f(x) as:
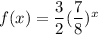
Here
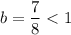
Hence, the function is a exponential decay function.
d)
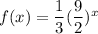
Here

Hence, the function is a exponential growth function.