Answer:
Option A is correct.
Explanation:
We need to find the product of

We know (a^2-b^2) = (a+b)(a-b)
so, (x^2-16) = (x)^2-(4)^2 = (x-4)(x+4)
2x+8 Taking 2 common from this term:
2x+8 = 2(x+4)
(x^3-2x^2+x) Taking x common from this term
x(x^2-2x+1) = x(x-1)^2 = x(x-1)(x-1)
(x^2+3x-4) factorizing this term
x^2+4x-x-4 = x(x+4)-1(x+4)
= (x-1)(x+4)
Now, Putting these simplified terms in the given equation:
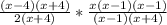
Now cancelling the same terms that are in numerator and denominator
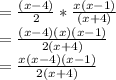
So, Option A is correct.