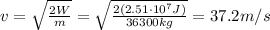Question

A 99.5 N grocery cart is pushed 12.9 m along an aisle by a shopper who exerts a constant horizontal force of 34.6 N. The acceleration of gravity is 9.81 m/s 2 . If all frictional forces are neglected and the cart starts from rest, what is the grocery cart’s final speed? Answer in units of m/s. 003 (part 1 of 4) 10.0 points In the 1950’s, an experimental train that had a mass of 36300 kg was powered across a level track by a jet engine that produced a thrust of 4.28 × 105 N for a distance of 586 m. Find the work done on the train. Answer in units of J. 004 (part 2 of 4) 10.0 points Find the change in kinetic energy. Answer in units of J. 005 (part 3 of 4) 10.0 points Find the final kinetic energy of the train if it started from rest. Answer in units of J. 006 (part 4 of 4) 10.0 points Find the final speed of the train assuming no friction. Answer in units of m/s.

Answer 1

1) 9.4 m/s

First of all, we can calculate the work done by the horizontal force, given by

W = Fd

where

F = 34.6 N is the magnitude of the force

d = 12.9 m is the displacement of the cart

Solving ,

W = (34.6 N)(12.9 m) = 446.3 J

According to the work-energy theorem, this is also equal to the kinetic energy gained by the cart:

`W=K_f - K_i`

Since the cart was initially at rest,
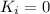`K_i = 0`, so

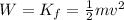`W=K_f = (1)/(2)mv^2` (1)

where

m is the of the cart

v is the final speed

The mass of the cart can be found starting from its weight,
`F_g = 99.5 N`:

`m=(F_g)/(g)=(99.5 N)/(9.8 m/s^2)=10.2 kg`

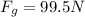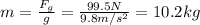
So solving eq.(1) for v, we find the final speed of the cart:

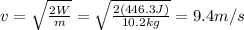
`v=\sqrt{(2W)/(m)}=\sqrt{(2(446.3 J))/(10.2 kg)}=9.4 m/s`

2)
`2.51\cdot 10^7 J`

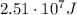
The work done on the train is given by

W = Fd

where

F is the magnitude of the force

d is the displacement of the train

In this problem,

`F=4.28 \cdot 10^5 N`

`d=586 m`

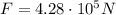
So the work done is

`W=(4.28\cdot 10^5 N)(586 m)=2.51\cdot 10^7 J`

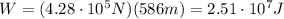
3)
`2.51\cdot 10^7 J`

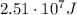
According to the work-energy theorem, the change in kinetic energy of the train is equal to the work done on it:

`W=\Delta K = K_f - K_i`

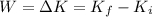
where

W is the work done

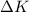`\Delta K` is the change in kinetic energy

Therefore, the change in kinetic energy is

`\Delta K = W = 2.51\cdot 10^7 J`

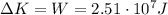
4) 37.2 m/s

According to the work-energy theorem,

`W=\Delta K = K_f - K_i`

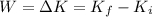
where

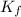`K_f` is the final kinetic energy of the train

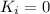`K_i = 0` is the initial kinetic energy of the train, which is zero since the train started from rest

Re-writing the equation,

`W=K_f = (1)/(2)mv^2`

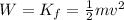
where

m = 36300 kg is the mass of the train

v is the final speed of the train

Solving for v, we find

`v=\sqrt{(2W)/(m)}=\sqrt{(2(2.51\cdot 10^7 J))/(36300 kg)}=37.2 m/s`