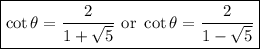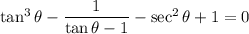
Recall that
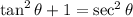 , so we can write everything in terms of
, so we can write everything in terms of
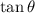 :
:
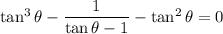
Let
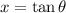 , so that
, so that
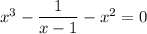
With some rewriting we get
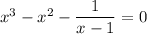
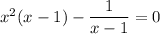
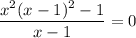
Clearly we cannot have
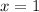 , or
, or
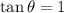 .
.
The numerator determines when the expression on the left reduces to 0:
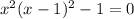
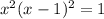
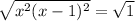
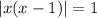
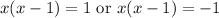
Completing the square gives
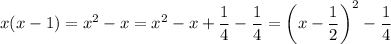
so that
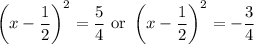
The second equation gives no real-valued solutions because squaring any real number gives a positive real number. (I'm assuming we don't care about complex solutions.) So we're left with only
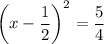
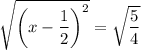
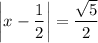
which again gives two cases,
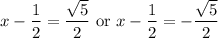
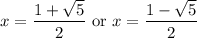
Then when
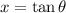 , we can find
, we can find
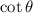 by taking the reciprocal, so we get
by taking the reciprocal, so we get