Answer: 12.10
Explanation:
Given : Mean :
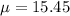
Standard deviation :
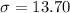
The formula to calculate the z-score :-
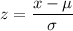
For x= 5 degrees
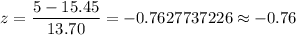
For x= 10 degrees
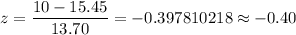
The P-value :
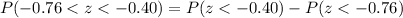
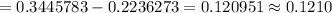
In percent ,
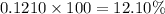
Hence, the percentage of days had a low temperature between 5 degrees and 10 degrees = 12.10%