Answer:
The sum of the six terms is 9331
Explanation:
* Lets explain what is the geometric sequence
- There is a constant ratio between each two consecutive numbers
- Ex:
# 5 , 10 , 20 , 40 , 80 , ………………………. (×2)
# 5000 , 1000 , 200 , 40 , …………………………(÷5)
* General term (nth term) of a Geometric sequence:
# U1 = a , U2 = ar , U3 = ar² , U4 = ar³ , U5 = ar^4
#
 , where a is the first term , r is the constant
, where a is the first term , r is the constant
ratio between each two consecutive terms, n is the position
of the term
- The sum of n terms of the geometric sequence is:
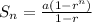 , where n is the number of the terms
, where n is the number of the terms
a is the first term and r is the common ratio
* Lets solve the problem
∵ The geometric sequence is 1 , -6 , 36 , .........
∵ The common ratio r = U2/U1
∵ U1 = 1 and U2 = -6
∴ r = -6/1 = -6
∵ The first term is 1
∴ a = 1
∵ There are 6 terms in the sequence
∴ n = 6
∴ The sum =
![(1[1 - (-6)^(6)])/(1-6)=(1[1-46656])/(-5)=(-46655)/(-5)=9331](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7csfvmbl0l7ahnxbe92nu2tkrllehb0mu1.png)
* The sum of the six terms is 9331