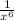Question 1:
We have the following expression:
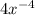
By definition of power properties we have to:
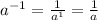
Then, rewriting the expression:
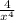
ANswer:
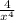
Question 2:
For this case we have the following expression:
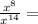
By definition of power properties of the same base we have:
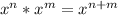
Then, we can rewrite the denominator of the expression as:
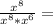
Simplifying terms of the numerator and denominator:
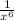
ANswer: