Question

Which series of transformations will NOT map figure L onto itself?

A. (x + 1, y − 4), reflection over y = x − 4
B. (x − 4, y − 4), reflection over y = −x
C. (x + 3, y − 3), reflection over y = x − 4
D. (x + 4, y + 4), reflection over y = −x + 8

Answer 1

A. (x + 1, y − 4), reflection over y = x − 4

Explanation:

The answer A. (x + 1, y − 4), reflection over y = x − 4 is right because I got it right on my test!! :)))

Answer 2

A. (x + 1, y − 4), reflection over y = x − 4

Explanation:

You must perform all the composed transformations to spot the one in which the coordinates of the preimage and the image are not the same.

The coordinates of the preimage are A(0,1), B(3,4), C(5,2) , and D(2,-1)

Option A is a translation (x + 1, y − 4), followed by a reflection over y = x − 4.

`A(0,1)\to(1,-3)\to A'(1,-3)`

`B(3,4)\to(4,0)\to B'(4,0)`

`C(5,2)\to(6,-2)\to C'(2,2)`

`D(2,-1)\to(3,-5)\to D'(-1,-1)`

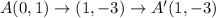
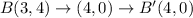
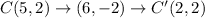
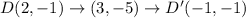
Option B is a translation (x − 4, y − 4), followed by a reflection over y = −x

`A(0,1)\to(-4,-3)\to A'(0,1)`

`B(3,4)\to(-1,0)\to B'(3,4)`

`C(5,2)\to(1,-2)\to C'(5,2)`

`D(2,-1)\to(-2,-5)\to D'(2,-1)`

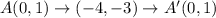
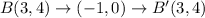
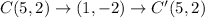
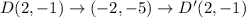
Option C is a translation (x +3, y − 3), followed by a reflection over y = x-4

`A(0,1)\to(3,-2)\to A'(0,1)`

`B(3,4)\to(6,1)\to B'(3,4)`

`C(5,2)\to(8,-1)\to C'(5,2)`

`D(2,-1)\to(5,-4)\to D'(2,-1)`

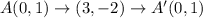
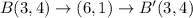
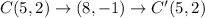
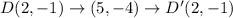
Option D is a translation (x +4, y + 4), followed by a reflection over y = −x+8

`A(0,1)\to(4,5)\to A'(0,1)`

`B(3,4)\to(7,8)\to B'(3,4)`

`C(5,2)\to(9,6)\to C'(5,2)`

`D(2,-1)\to(6,3)\to D'(2,-1)`

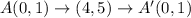
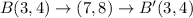
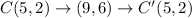
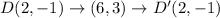
The correct choice is A.