Answer:
Area of the rectangle is increasing with the rate of 84 cm/s.
Explanation:
Let l represents the length, w represents width, t represents time ( in seconds ) and A represents the area of the triangle,
Given,
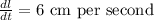

Also, l = 12 cm and w = 4 cm,
We know that,
A = l × w,
Differentiating with respect to t,
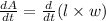
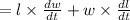
By substituting the values,
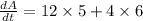
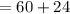
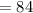
Hence, the area of the rectangle is increasing with the rate of 84 cm/s.