Answer:
Explanation:
we have the system :
8x+4y=16
7y=15
the easiest unknown to find first is y because we have the second equation contains only y :
7y=15 we divide both sides by 7 we get : y=
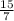
then we can substitute this value in the first equation to find x :
8x+4
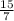 = 16
= 16
means : 8x+
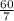 = 16
= 16
8x=16-
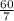
8x =
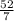
divide both sides by 8 :
x =
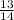
so the solution is (
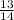 ,
,
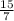 )
)
this is the solution of the system you submitted
Now if you meant this system :
8x+4y=16
7y=15-1
we get :
7y=14 which gives us y=2
then 8x+4(2)=16 gives us : 8x+8=16
means 8x=8
means x=1
and in this case the solution will be (1,2) answer C