Answer:
Third choice from the top is the one you want
Explanation:
This whole concept relies on the fact that if the index of a radical exactly matches the power under the radical, both the radical and the power cancel each other out. For example:
![\sqrt[6]{x^6} =x](https://img.qammunity.org/2020/formulas/mathematics/high-school/uhgn7ni8hh1pgqts58xzuj0lp1vsshw1nc.png) and another example:
and another example:
![\sqrt[12]{2^(12)}=2](https://img.qammunity.org/2020/formulas/mathematics/high-school/a0xitj5pqjs7lpmaqtm7e2p9rsro4677wq.png)
Let's take this step by step. First we will rewrite both the numerator and the denominator in rational exponential equivalencies:
![\frac{\sqrt[4]{6} }{\sqrt[3]{2} }=\frac{6^{(1)/(4) }}{2^{(1)/(3) }}](https://img.qammunity.org/2020/formulas/mathematics/high-school/22zrnr04w3gu5abt61gw8awtvxp0igbk2t.png)
In order to do anything with this, we need to make the index (ie. the denominators of each of those rational exponents) the same number. The LCM of 3 and 4 is 12. So we rewrite as
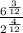
Now we will put it back into radical form so we can rationalize the denominator:
![\frac{\sqrt[12]{6^3} }{\sqrt[12]{2^4} }](https://img.qammunity.org/2020/formulas/mathematics/high-school/r94a56cvgwtkp1mbgj4axqflxyd8e67vi9.png)
In order to rationalize the denominator, we need the power on the 2 to be a 12. Right now it's a 4, so we are "missing" 8. The rule for multiplying like bases is that you add the exponents. Therefore,
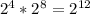
We will rationalize by multiplying in a unit multiplier equal to 1 in the form of
![\frac{\sqrt[12]{2^8} }{\sqrt[12]{2^8} }](https://img.qammunity.org/2020/formulas/mathematics/high-school/s5edfqvjdhmtfqblwlsii2rl43kc8gb1yl.png)
That looks like this:
![\frac{\sqrt[12]{6^3} }{\sqrt[12]{2^4} }*\frac{\sqrt[12]{2^8} }{\sqrt[12]{2^8} }](https://img.qammunity.org/2020/formulas/mathematics/high-school/ynkqrqc73qjaxonufgmkwqutiornxjthr3.png)
This simplifies down to
![\frac{\sqrt[12]{216*256} }{\sqrt[12]{2^(12)} }](https://img.qammunity.org/2020/formulas/mathematics/high-school/nq0e6mhoe3of1iqu8a1ehbt1vnb499ni2h.png)
Since the index and the power on the 2 are both 12, they cancel each other out leaving us with just a 2! Doing the multiplication of those 2 numbers in the numerator gives us, as a final answer:
![\frac{\sqrt[12]{55296} }{2}](https://img.qammunity.org/2020/formulas/mathematics/high-school/tbc41o9ix7nmfuudth958ds7tzavsv14wz.png)
Phew!!!