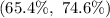Question

Out of 100 students sampled, 70 of them said that they hoped to get married someday. With 68% confidence, what is the approximate percentage of the students in the population who hope to get married someday?

Answer 1

Answer:
`(65.4\%,\ 74.6\%)`

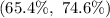
Explanation:

Given : Out of 100 students sampled, 70 of them said that they hoped to get married someday.

i.e. Sample size : n= 100 and Sample proportion:
`\hat{p}=(70)/(100)=0.7`

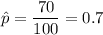
Using standard normal table for z,

Critical z-value(two-tailed) for 68% confidence =
`z_(\alpha/2)=0.9945`

Now, confidence interval for population proportion:-

`\hat{p}\pm z_(\alpha/2)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\\\\=0.7\pm(0.9945)\sqrt{((0.7)(0.3))/(100)}\\\\=0.7\pm0.0455737152863\\\\\approx0.7\pm0.046\\\\=(0.7-0.046,\ 0.7+0.046)=(0.654,\ 0.746)\\\\=(65.4\%,\ 74.6\%)`

Hence, the approximate percentage of the students in the population who hope to get married someday =
`(65.4\%,\ 74.6\%)`

Answer 2

65.4% to 74.6%

Explanation:

68% is approximately plus minus 1 standard deviations.

sigma=sqrt(n*p*(1-p))=sqrt(100*.7*.3)=4.58

so we're looking at 70+4.6 and 70-4.6.