Question

Find the mass of the lamina that occupies the region D = {(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1} with the density function ρ(x, y) = xye^(x+y)

Answer 1

The mass of the lamina is 1

Explanation:

Let
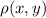`\rho(x,y)` be a continuous density function of a lamina in the plane region D,then the mass of the lamina is given by:

`m=\int\limits \int\limits_D \rho(x,y) \, dA`.

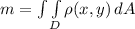From the question, the given density function is
`\rho (x,y)=xye^(x+y)`.

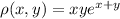Again, the lamina occupies a rectangular region: D={(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1}.

The mass of the lamina can be found by evaluating the double integral:

`I=\int\limits^1_0\int\limits^1_0xye^(x+y)dydx`.

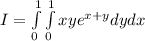Since D is a rectangular region, we can apply Fubini's Theorem to get:

`I=\int\limits^1_0(\int\limits^1_0xye^(x+y)dy)dx`.

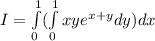Let the inner integral be:
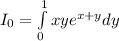`I_0=\int\limits^1_0xye^(x+y)dy`, then

`I=\int\limits^1_0(I_0)dx`.

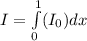The inner integral is evaluated using integration by parts.

Let
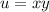`u=xy`, the partial derivative of u wrt y is

`\implies du=xdy`

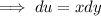
and

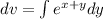`dv=\int\limits e^(x+y) dy`, integrating wrt y, we obtain

`v=\int\limits e^(x+y)`

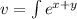
Recall the integration by parts formula:
`\int\limits udv=uv- \int\limits vdu`

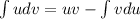
This implies that:

`\int\limits xye^(x+y)dy=xye^(x+y)-\int\limits e^(x+y)\cdot xdy`

`\int\limits xye^(x+y)dy=xye^(x+y)-xe^(x+y)`

`I_0=\int\limits^1_0 xye^(x+y)dy`

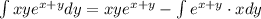
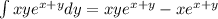
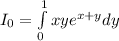
We substitute the limits of integration and evaluate to get:

`I_0=xe^x`

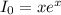
This implies that:

`I=\int\limits^1_0(xe^x)dx`.

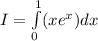Or

`I=\int\limits^1_0xe^xdx`.

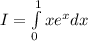We again apply integration by parts formula to get:

`\int\limits xe^xdx=e^x(x-1)`.

`I=\int\limits^1_0xe^xdx=e^1(1-1)-e^0(0-1)`.

`I=\int\limits^1_0xe^xdx=0-1(0-1)`.

`I=\int\limits^1_0xe^xdx=0-1(-1)=1`.

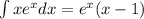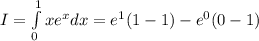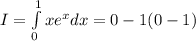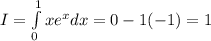No unit is given, therefore the mass of the lamina is 1.