Answer:
The mass of the lamina is 1
Explanation:
Let
 be a continuous density function of a lamina in the plane region D,then the mass of the lamina is given by:
be a continuous density function of a lamina in the plane region D,then the mass of the lamina is given by:
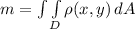 .
.
From the question, the given density function is
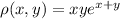 .
.
Again, the lamina occupies a rectangular region: D={(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1}.
The mass of the lamina can be found by evaluating the double integral:
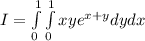 .
.
Since D is a rectangular region, we can apply Fubini's Theorem to get:
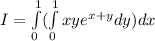 .
.
Let the inner integral be:
 , then
, then
 .
.
The inner integral is evaluated using integration by parts.
Let
 , the partial derivative of u wrt y is
, the partial derivative of u wrt y is
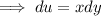
and
 , integrating wrt y, we obtain
, integrating wrt y, we obtain
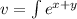
Recall the integration by parts formula:

This implies that:

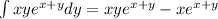
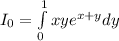
We substitute the limits of integration and evaluate to get:
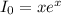
This implies that:
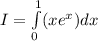 .
.
Or
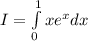 .
.
We again apply integration by parts formula to get:
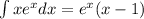 .
.
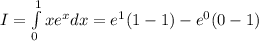 .
.
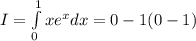 .
.
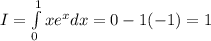 .
.
No unit is given, therefore the mass of the lamina is 1.