Answer:
Exponential decay, 55% decrease
Explanation:

General exponential growth function is
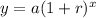
exponential growth function is
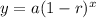
The value of 1-r is less than 1 then it is exponential decay
In the given f(x) , the 1-r is 0.45 that is less than 1
So it is exponential decay.
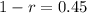
Subtract 1 on both sides
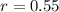
Multiply by 100 to get %
r= 55%
Exponential decay, 55% decrease