Answer:
x = 1
Explanation:
We are to find the solution of the following logarithmic equation:
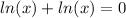
We will add the similar elements to get:
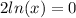
Dividing both sides by 2 and simplify to get:
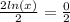
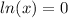
Applying the rule
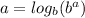 to get:
to get:
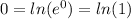
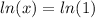
Here the logs have the same base, so:
x = 1