Question

What is the solution to this Logarithmic Equation?

(Those are L's infront of the N)
ln x + ln x = 0

Answer 1

x = 1

Explanation:

ln x + ln x = 0

2ln x = 0

ln x = 0

recall ln x =
`log_(e)`x

so equation becomes

`log_(e)`x = 0

or
`e^(0)`=x

since anything raised to the power of zero = 1

x = 1

Answer 2

x = 1

Explanation:

We are to find the solution of the following logarithmic equation:

`ln ( x ) + l n ( x ) = 0`

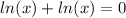
We will add the similar elements to get:

`2 l n ( x ) = 0`

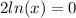
Dividing both sides by 2 and simplify to get:

`\frac { 2 l n ( x ) } { 2 } = \frac { 0 } { 2 }`

`ln(x)=0`

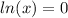
Applying the rule
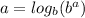`a=log_b(b^a)` to get:

`0=ln(e^0)=ln(1)`

`ln(x)=ln(1)`

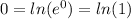
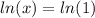
Here the logs have the same base, so:

x = 1