Question

An object moving at a constant speed of 29 m/s is making a turn with a radius of curvature of 9 m (this is the radius of the "kissing circle"). The object's momentum has a magnitude of 61 kg·m/s. What is the magnitude of the rate of change of the momentum?

Answer 1

The rate of change of the momentum is 196.5 kg-m/s²

Step-by-step explanation:

Given that,

Speed v = 29 m/s

Radius = 9 m

Momentum = 61 kg-m/s

We need to calculate the rate of change of the momentum

Using formula of momentum

`F = (\Delta p)/(\Delta t)`

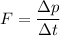
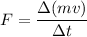`F=(\Delta(mv))/(\Delta t)`.....(I)

Using newtons second law

`F = ma=m(v^2)/(r)`

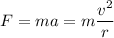
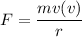`F = (mv(v))/(r)`....(II)

From equation (I) and (II)

`(\Delta p)/(\Delta t)=(61*29)/(9)`

`(\Delta p)/(\Delta t)=196.5\ kg-m/s^2`

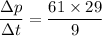
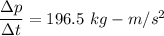
Hence, The rate of change of the momentum is 196.5 kg-m/s²