Answer with explanation:
(a)
Mean number of flight hours for Continental Airline pilots = 49 hours per month
Total Sample Size =100
Standard Deviation =11.5 Hours
Margin of error for a 95% confidence interval
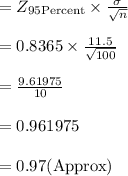
(b)
The Range of values for a 95% confidence interval
⇒ Mean number of flight + Margin of Error ≤ Confidence interval ≤ Mean number of flight - Margin of Error
⇒ 49+0.97 ≤ Confidence interval ≤ 49-0.97
⇒ 49.97 ≤ Confidence interval ≤48.03
Upper Bound = 49.97